Le deep learning a marqué l’année 2023, avec le succès fulgurant des modèles de langage (LLMs) tels que ChatGPT (OpenAI)[1], Gemini (Google)[2], LLaMA (Facebook)[3]. Ces modèles, entraînés sur d’énormes quantités de données textuelles, parviennent à approximer la distribution probabiliste de leurs données d’entraînement, ce qui leur permet de générer un texte pertinent et cohérent avec leurs données d’entraînement.
L’un des ingrédients principaux de la réussite de ces modèles est la quantité massive de données d’entraînement, environ 1,56 To (pour Bard de Google), ce qui soulève la question de l’applicabilité du deep learning dans certains domaines où la quantité de données est très limitée.
Dans de nombreux domaines industriels, les équations différentielles jouent un rôle clé dans la modélisation des différents paramètres du système industriel en question. Par exemple, dans l’aéronautique, les écoulements de fluides, l’ingénierie du bâtiment et la prédiction météorologique, la résolution des équations différentielles est une étape cruciale dans le processus de modélisation. La résolution de la majorité de ces équations différentielles est effectuée aujourd’hui en utilisant des méthodes basées sur la discrétisation de ces équations, telles que les éléments finis, les différences finies et les volumes finis.
Cependant, ces méthodes de résolution deviennent très coûteuses en temps de calcul (en heures, jours, semaines) dans le cas où les équations différentielles sont multidimensionnelles, à plusieurs variables et avec un grand nombre de points de résolution, ce qui est souvent le cas dans la majorité des applications industrielles.
Cette limitation en temps de calcul allonge considérablement les temps d’étude scientifique et limite (ou rend même impossible) l’utilisation de certaines techniques d’optimisation qui nécessitent plusieurs résolutions de l’équation différentielle, telles que la MCMC (Markov Chain Monte Carlo) dans le cadre des problèmes inverses.
Dans ce contexte, où l’on est confronté à des problèmes caractérisés par une grande dimensionnalité, et une forte non-linéarité, le deep learning peut représenter un bon candidat, compte tenu de ses succès dans les domaines des LLMs, de la vision par ordinateur et de la découverte de médicaments.
Cependant, les données ne sont pas aussi abondantes que dans le cas des LLMs, en raison du coût élevé des méthodes conventionnelles de résolution des équations différentielles (en heures, jours, semaines). Cela risque de poser un problème pour les approches deep learning, qui sont réputées pour être gourmandes en données d’entraînement.
Malgré cette limitation théorique, plusieurs approches deep learning ont été proposées pour la résolution d’équations différentielles. Le principal avantage attendu d’une solution de deep learning est la réduction significative du temps de calcul, passant d’un ordre de grandeur de plusieurs heures, jours ou semaines à un ordre de grandeur de quelques secondes.
L’avantage précédent s’explique par le fait que les méthodes de résolution classiques (éléments finis, différences finies, volumes finis) résolvent littéralement l’équation différentielle à chaque appel (discrétisation, résolution de systèmes linéaires, etc.). La solution deep learning effectue simplement une évaluation directe de la solution approximée de l’équation différentielle apprise pendant la phase d’apprentissage (pas de résolution de systèmes linéaires).
Comment la solution de deep learning est-elle construite ? Selon l’état de l’art, deux solutions sont possibles :
– Approximation avec des données de simulation (I):
Cette famille d’approches, nécessitent au préalable, de générer quelques simulations de l’équation différentielle, que l’on souhaite résoudre. Généralement le nombre de simulations est de l’ordre de quelques centaines de simulations (M = 500, 1000, 1500, …) . Les différentes variables inconnues de l’équation différentielle sont modélisées par une architecture deep learning. Example dans l’équation (1) ci-dessous les différentes variables inconnues sont u_1,…,u_N, régies par l’ équation différentielle ED (e.g. Navier-stockes)
Dans (1) et (2), x regroupe tous les paramètres statiques (coordonnées spatiales, …) t représente la coordonnée temporelle.
Une solution deep learning modélise le vecteur des variables inconnues U par un réseau deep learning noté Û équation (2). Durant la phase d’apprentissage, on minimise l’écart entre Û et U via une fonction coût notée L (3).
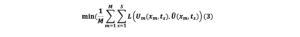
Dans l’équation (3) U_m est la m -ème simulation de l’équation différentielle ED. U ̂(x_m,t) Est la réponse correspondante générée par le réseau de neurones (voir Figure 1).
Dans la modélisation précédente le paramètre est donné directement comme entrée à l’architecture , dans d’autres formulations le temps peut être passé implicitement en donnant comme entrée la prédiction au pas de temps précédent 
(réseaux récurrents).
Un exemple de cette famille d’approches a été introduit dans l’article [4]. Les auteurs ont introduit une nouvelle architecture deep learning basée sur les opérateurs de Fourier pour résoudre des équations différentielles paramétrisées.
L’idée de cet article est d’utiliser le théorème de convolution (4) pour passer d’une convolution classique à une convolution dans l’espace de Fourier.
Ce passage présente deux avantages ; primo, une convolution dans l’espace Fourier (multiplication) est plus rapide à calculer qu’une convolution classique (convolution). Secundo, une convolution dans l’espace Fourier a un nombre de modes infinis non paramétrisés alors qu’une convolution classique présente un nombre de mode finis et paramétrisés ce qui limiter leur capacité d’apprentissage, en plus d’augmenter le nombre de paramètre de l’architecture.
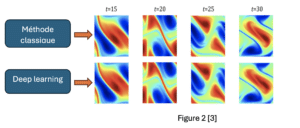
La Figure 2 illustre la performance de l’architecture introduite dans [4] comparée à une méthode de résolution classique. Les équations différentielles en question sont les équations de Navier-Stockes. Dans ce cas M =1000 simulations ont été utilisées pour entrainer l’architecture deep learning.
Au niveau du temps de calcul, et pour effectuer 30.000 simulations il nous faut 2.2 minutes avec l’approche basée sur le deep learning dans [4] alors qu’une approche traditionnelle il faut compter 18 heures de temps de calcul !!! cet exemple montre que le deep learning peut être utilisé efficacement pour résoudre des équations différentielles avec un temps de calcul nettement inférieur à celui des méthodes classiques, ceci, tout en gardant une excellente qualité de prédiction.
- Approximation avec des données de simulation + la physique (II):
La famille d’approche précédente essaye d’approximer la solution de l’équation différentielle en utilisant quelques simulations générées avec une méthode de résolution classique. L’inconvénient de l’approche précédente est le faite que l’équation différentielle ne soit pas prise en compte pendant le process d’apprentissage, ceci risque de ne pas garantir le respect de l’équation différentielle des solutions obtenues à partir du deep learning.
Une autre famille d’approches basée sur la méthode (Physics informed neural netwroks : PINNs)[5] présente un nouveau cadre de résolution des équations différentielles. Les PINNs prennent en compte l’équation différentielle durant la phase d’apprentissage. La fonction coût des PINNs est composée de deux parties ; une partie pour les simulations observées et une autre partie pour l’équation différentielle.
Une discrétisation des espaces 
est nécessaire
. Ces derniers points sont appelés des points de colocations. C’est sur ces points que la fonction cout équation différentielle sera évaluée (deuxième partie de l’équation (3)). ß est un hyperparamètre important dans l’apprentissage PINNs, il contrôle l’apport de la fonction coût équation différentielle.
L’apprentissage des PINNs est guidée par l’équation différentielle. L’inclusion de la fonction coût équation différentielle peut être aussi vu comme une forme de régularisation de la fonction coût global, ce qui peut être bénéfique pour une meilleure généralisation des solutions.
Le calcul de dérivées dans la fonction coût équation différentielle ne nécessite aucune méthode de discrétisation et peut être obtenu directement grâce à la méthode de différence automatique avec le théorème de dérivation des fonctions composées.
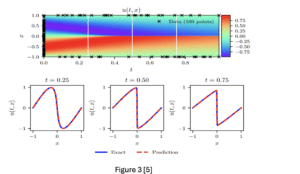
Dans la Figure 3, les auteurs du [5], montrent que les PINNs arrivent à résoudre l’équation de Burger [6] avec une erreur de mesure de l’ordre 
(en norme 2). Dans ce cas M=100 et P*Q =10000.
Dans l’article [7] les auteurs ont introduit une architecture deep learning pour modéliser la réponse d’un bâtiment sous l’effet d’un séisme. Un tel comportement peut être modéliser par l’équation différentielle suivante :
est la masse du bâtiment.
sont respectivement le déplacement, la vitesse et l’accélération du bâtiment à la suite d’un mouvement du sol représenté par 
. Les inconnus principaux sont le déplacement, la vitesse et la fonction g ;
.
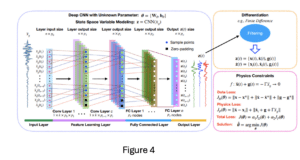
Figure 4, illustre l’architecture deep learning [PhyCNNs] introduite dans [7]. L’architecture se base sur des réseaux de convolutions(1D) suivis par des réseaux fully-connected.
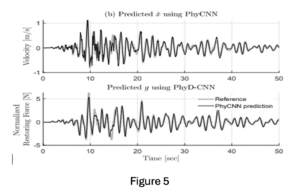
La Figure 5 illustre la performance de l’architecture PhyCNNs en comparant la prédiction obtenue avec PhyCNNs et la référence obtenue avec une méthode de résolution classique.
Dans l’approche PINNs, on utilise généralement une architecture deep learning type réseau de neurones « fully-conneceted » . Ce type d’architecture nous permet dériver facilement à n’importe l’ordre de dérivées, ceci en utilisant la différence automatique et le théorème de dérivation des fonctions composées. D’autres architectures deep learning peuvent être utilisées (réseaux convolutifs), exemple article [7], dans ce cas il faut utiliser une méthode de différence finie pour estimer les dérivées, ce qui peut rapidement devenir très couteux dans le cas des grandes dimensions et des ordres de dérivées très élevés.
Les approches type « PINNs » (II) sont généralement moins gourmandes en données de simulation comparées à la première famille d’approche (I), ceci est grâce à l’inclusion de l’équation différentielle dans l’apprentissage. En revanche leur temps d’apprentissage est beaucoup plus élevé que celui de la première approche (I). Ceci est dû au nombre de points de colocation. Ce nombre augmente très rapidement avec la dimension des variables. En plus, le choix de la discrétisation des points de colocation n’est pas évident.
Dans les cas où les données de simulation ne proviennent pas directement de l’équation différentielle, par exemple, elles ont été mesurées directement sur le terrain, ces données ne sont pas nécessairement conformes à l’équation différentielle (erreur de mesure, équipement de mesure différent, etc.), cela risque de créer un conflit entre la fonction coût équation différentielle et la fonction coût données de simulation.
En conclusion, la première approche est plus flexible que l’approche PINNs (fonction coût plus simple, entrainement plus facile, indépendance de l’équation différentielle), avec seulement quelques simulations on peut approximer une solution de l’équation différentielle. Cependant, ne pas inclure l’équation différentielle dans le processus d’apprentissage, risque de donner des solutions qui ne respectent pas la physique. L’approche PINNs, de l’autre côté, inclus l’équation différentielle dans le processus d’apprentissage, ce qui permet de réduire le nombre de simulations nécessaires à l’apprentissage, régularisation de l’apprentissage, et aussi garantir des solutions qui respectent l’équation différentielle. Cependant, l’apprentissage PINNs est moins évident que celui de la première approche (temps d’apprentissage, tuning d’hyperparamètres, conformité entre la physique et les données d’apprentissage), dans la table en dessous on résume la comparaison entre les deux approches.
| Approche (I) | Approche (II) | |
| Difficulté d’apprentissage | Facile (+) | Intermédiaire/difficile (-) |
| Respect de la physique | Pas garantie (-) | Garantie grâce à l’ED (+) |
| Quantité de données | Plus de données (-) | Moins de données (+) |
| Temps d’apprentissage | Intermédiaire (+) | Long (-) |
Table : comparaison entre les deux approches
[1]: https://openai.com/research/gpt-4
[2]: https://gemini.google.com/app?hl=fr
[3] : https://llama.meta.com/llama3/
[4]: Fourier Neural Operator for Parametric Partial Differential Equations, Zongyi Li and Nikola Kovachki and Kamyar Azizzadenesheli and Burigede Liu and Kaushik Bhattacharya and Andrew Stuart and Anima Anandkumar, 2021, arxiv
[5]: Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations, Maziar Raissi and Paris Perdikaris and George Em Karniadakis, 2017, arXiv
[6]: C. Basdevant, M. Deville, P. Haldenwang, J. Lacroix, J. Ouazzani, R. Peyret, P. Orlandi, A. Patera, Spectral and finite difference solutions of the Burgers equation, Computers & fluids 14 (1986) 23–41.
Abderrahmane Yewgat 
