Active Learning et Semi-Supervised Learning
Retrouvez toutes nos autres videos sur notre chaîne YouTube.
Dans le cadre de l’apprentissage supervisé, l’entraînement d’un réseau de neurones repose sur l’exploitation d’un ensemble de données dites labellisées, i.e. qui contiennent des informations permettant de guider l’entraînement du modèle. Dans le cas d’un problème de classification d’images par exemple, “labelliser” revient à indiquer à quelle classe (label) appartient l’objet représenté sur chaque image (input).
En pratique, le travail de labellisation pouvant s’avérer laborieux et coûteux, il n’est pas rare que seule une (petite) partie des données acquises ait été labellisée. Dans quelle mesure peut-on alors tirer profit des données non labellisées pour optimiser les performances du modèle ? C’est la question à laquelle l’apprentissage semi-supervisé (ou semi-supervised learning (SSL)) d’une part, et l’active learning (AL) d’autre part se proposent d’apporter une réponse.
Ces deux domaines émergents de l’IA sont à l’origine d’une littérature florissante qui laisse entrevoir des perspectives particulièrement prometteuses pour l’avenir du deep learning. Dans cet article, nous proposons un aperçu des différentes stratégies de SSL et d’AL respectivement. La liste des méthodes présentées n’a pas pour vocation d’être exhaustive, mais plutôt de permettre une compréhension intuitive des concepts les plus récurrents dans la littérature dédiée. Les articles cités sont mentionnés à simple titre d’exemple.
I. APPRENTISSAGE SEMI-SUPERVISÉ
L’apprentissage semi-supervisé consiste à entraîner un (ou plusieurs) modèle(s) en incorporant les données non labellisées à l’ensemble d’apprentissage. En d’autres termes, non seulement l’entraînement s’effectue-t-il sur les données labellisées à disposition, mais les modifications successives du modèle sont également largement influencées par l’information extraite des données non labellisées. Les différentes techniques développées dans cette direction peuvent globalement se répartir en quatre grandes catégories, dont nous dressons le portrait ci-dessous.
A. Self-training
Une première approche, relativement intuitive, consiste à appliquer ce que l’on appelle pseudo-labeling ou self-training. En substance, cette technique revient à considérer les prédictions faites par le modèle sur les données non labellisées comme de nouveaux labels dont le modèle pourra se servir pour affiner son apprentissage.
En pratique, le self-training est mis en œuvre comme suit : tout d’abord, un modèle est entraîné en mode supervisé sur les données labellisées seulement. Il est ensuite appliqué aux données non labellisées, générant ainsi une prédiction pour chacun des échantillons. Si la prédiction est générée avec un score de confiance suffisamment élevé, il est supposé que c’est une prédiction fiable. La paire échantillon-prédiction peut alors être incorporée à l’ensemble d’apprentissage, la prédiction faisant office de label (on parle de pseudo-label). Le modèle peut alors être réentraîné en mode supervisé sur l’ensemble de données labellisées et pseudo-labellisées.
Une approche similaire et particulièrement populaire parmi les méthodes de SSL suggère d’entraîner non pas un modèle, mais deux (ou plus) conjointement afin d’obtenir une solution finale plus robuste et moins biaisée. C’est ce que l’on appelle le co-training [5]. Le plus souvent, cette stratégie met en œuvre un premier modèle, dit enseignant, dont le rôle est de générer les pseudo-labels qui serviront à entraîner le deuxième modèle, dit élève. Une fois ce dernier entraîné, le modèle enseignant peut être modifié en s’inspirant de l’élève, et générer de nouveau des pseudo-labels. Ce cycle, qui peut être répété autant de fois que souhaité, est illustré en figure 1.
Le plus souvent, ces techniques reposent sur l’utilisation de différentes augmentations (i.e. perturbations) des inputs, et se fondent sur l’hypothèse qu’un modèle devrait produire des prédictions similaires lorsqu’il est appliqué à des versions perturbées d’un même échantillon (consistency regularization [3]).
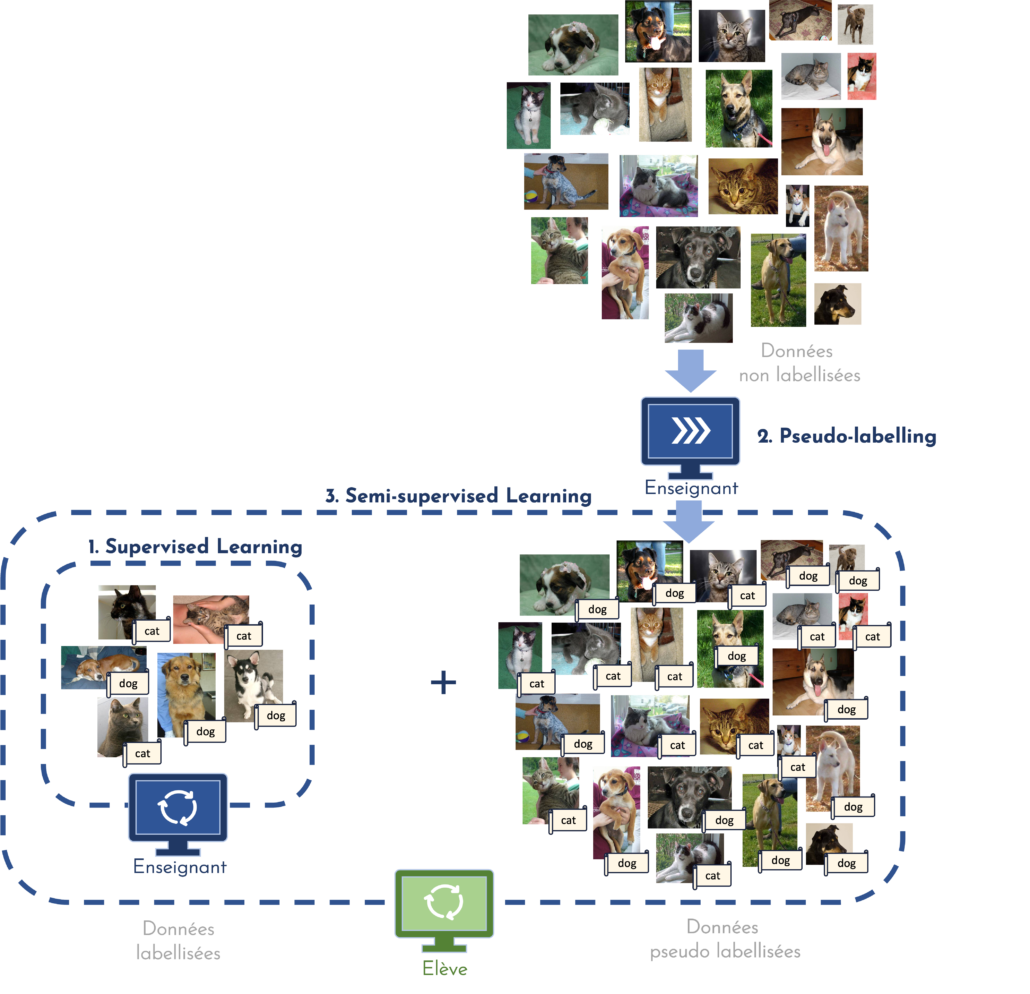
[FIGURE 1 ] – Illustration du co-training : le modèle enseignant génère des pseudo-labels qui serviront à l’entraînement du modèle élève.
B. Modèles génératifs
Une autre grande famille d’approches SSL se fonde sur une méthode statistique faisant intervenir conjointement un modèle génératif et un modèle discriminatif. (Par abus de langage, on parle simplement de modèles génératifs.)
De façon générale, les approches générative et discriminative permettent toutes deux de répondre à des problématiques de classification automatique via la modélisation statistique de variables d’intérêt. C’est le choix de la distribution de probabilité à estimer qui distingue les deux approches, et confère à l’une et l’autre des propriétés diverses. En particulier, un modèle génératif pourra servir, comme son nom l’indique, à générer de nouvelles données selon la distribution qu’il aura modélisé ; un modèle discriminatif pourra quant à lui être employé pour “discriminer” ou classifier un nouvel échantillon.
Les réseaux adversaires génératifs, abrégés GANs en anglais, sont un exemple intéressant de l’utilisation synchrone de ces deux types de modèles. Concrètement, on place deux réseaux de neurones en compétition selon un scénario de théorie des jeux. Le premier réseau est dit générateur, il est chargé de générer de nouveaux échantillons. Le réseau adversaire, dit discriminateur, a lui pour mission de déterminer si un échantillon est réel ou s’il a été produit par le générateur. Souvent, l’intérêt d’un GAN réside dans son générateur, qui pourra, une fois entraîné, générer de nouveaux échantillons (par exemple des images) particulièrement réalistes.
En apprentissage semi-supervisé, c’est plutôt le discriminateur que l’on souhaite utiliser à la fin de l’apprentissage, puisqu’il fera office de classifieur [1]. Son entraînement se déroule en deux temps (illustration en figure 2). Au cours de la première étape, le générateur et le discriminateur sont entraînés conjointement, de la même façon que pour un GAN standard. Cette étape se fait en mode non-supervisé : les images réelles fournies au discriminateur lors de son apprentissage sont en effet non labellisées. Cette phase permet au discriminateur d’apprendre à extraire les caractéristiques importantes des échantillons pour discriminer correctement les images réelles des fausses. Il pourra se servir de cette capacité d’extraction lors de la seconde phase, supervisée. Cette fois, le discriminateur ne reçoit en entrée que des images réelles labellisées. Sa mission : apprendre à classifier correctement ces images. Ce type de méthodes offre donc la possibilité d’entraîner un classifieur en exploitant aussi bien les données labellisées que non labellisées.
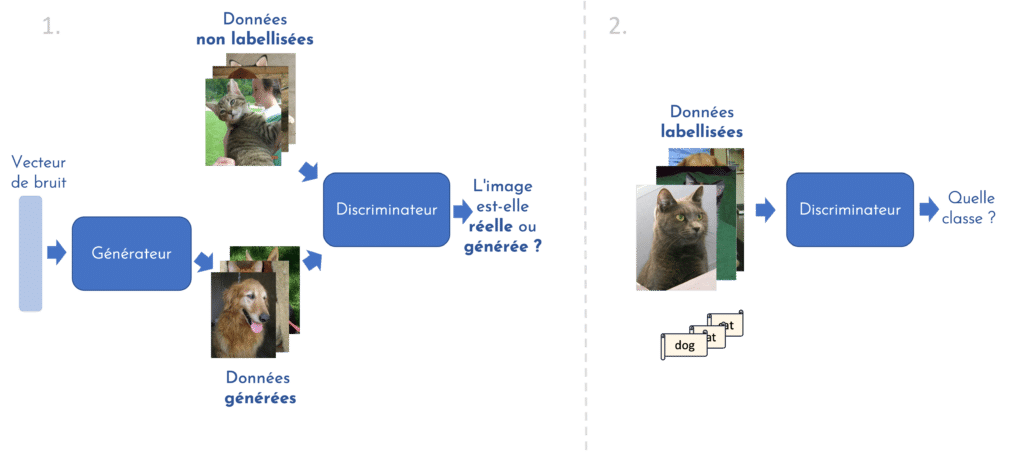
[FIGURE 2] – Entraînement d’un GAN en modes non-supervisé et supervisé pour obtenir un discriminant pouvant jouer le rôle d’un classifieur.
C. Séparation de faible densité
Parmi les approches SSL, on compte également celles dites de low-density separation, ou séparation de faible densité. Ces méthodes se fondent sur l’hypothèse que les frontières de séparation des différentes classes ne doivent pas traverser des zones à forte densité.
Pour mieux appréhender cette idée, observons la figure 3. Admettons que nous ayons pour but de tracer une ligne délimitant l’espace des “+” (vert) de l’espace des “-” (rouge). Dans le premier cas (à gauche), nous n’exploitons que les données labellisées (i.e les points rouges et verts) pour entraîner un modèle supervisé. Résoudre ce problème est ardu, puisqu’il existe une infinité de possibilités pour séparer les “+” des “-”, et le peu de données à disposition ne permet pas de déduire la classe d’appartenance d’un nouveau point (jaune). Dans le deuxième cas (à droite), nous choisissons de mettre l’information extraite des données non labellisées (bleu) à profit afin d’améliorer les performances de notre classifieur. Cette fois, tracer la ligne de séparation semble beaucoup facile, même si les données ne sont pas toutes labellisées : intuitivement, on s’attend à ce que les zones à forte concentration portent le même label. Dans notre exemple, on pourra conclure que le point à classifier (jaune) appartient avec une forte probabilité à la classe des “+” (vert).
C’est sur ce concept que se basent les méthodes de séparation de faible densité, parmi lesquelles se trouvent les Transductive SVMs ou Semi-supervised SVMs (S3VMs)[2]. Cette technique incorpore à l’algorithme de SVMs standard, conçue pour répondre à la problématique de classification dans un contexte supervisé, une contrainte encourageant le clustering (i.e. un regroupement pertinent) des données non labellisées.
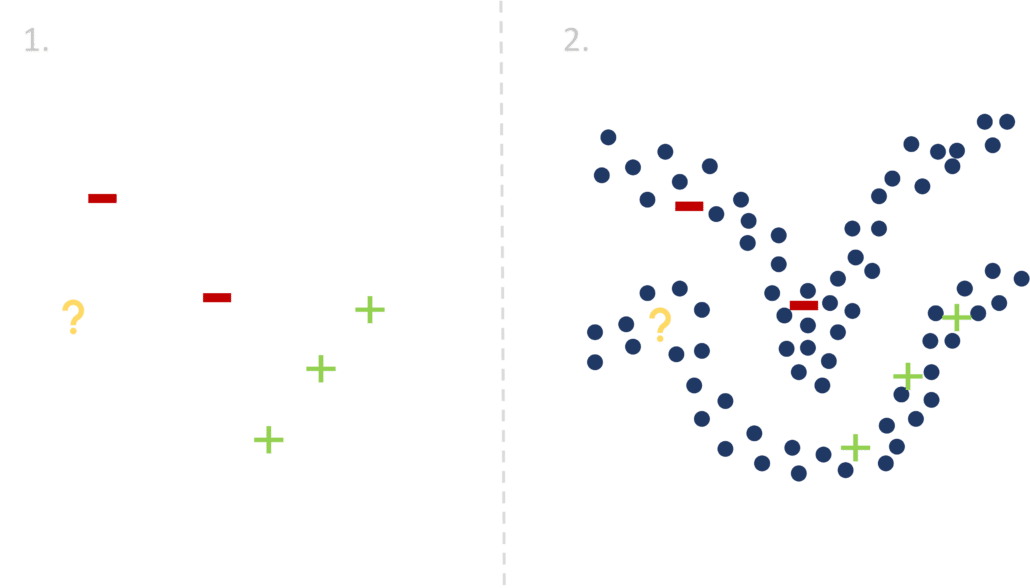
[FIGURE 3] – Illustration de l’information utile pouvant être contenue dans les données non labellisées (en bleu) face à un problème de classification (points labellisés en rouge et vert).
D. Graphes
Une dernière catégorie parmi celles que nous souhaitons évoquer ici est celle des méthodes basées sur les graphes. L’idée fondatrice de ce type d’approches tient essentiellement à l’hypothèse que des données similaires devraient présenter le même label. Cette conjecture rejoint les concepts présentés dans la sous-section précédente, mais est ici exploitée sous la forme d’un graphe (ajoutant donc la notion de connexion entre les échantillons).
En pratique, cette approche se déroule en deux temps :
- Construction du graphe : pour ce faire, une métrique de similarité doit être déterminée. Elle peut être choisie au préalable (par ex. : la distance euclidienne entre les représentations des inputs dans un espace latent) ou apprise de façon non-supervisée. Une fois cette métrique choisie, elle peut être utilisée pour quantifier la similarité de chaque paire d’échantillons. C’est ainsi que l’on peut mettre en place un graphe dans lequel les nœuds représentent les échantillons (ex: images) et les arêtes, plus ou moins épaisses, symbolisent la similarité plus ou moins forte entre ceux-ci. Cette première étape se déroule en mode non supervisé, elle ne fait pas appel aux labels.
- Prédiction des labels : il s’agit désormais d’exploiter les labels disponibles en s’appuyant sur la structure du graphe pour prédire la classe des échantillons non-labellisés. Parmi les techniques existantes, on peut notamment citer la Label propagation [9] qui, comme son nom l’indique, “propage” les labels et affecte à chaque échantillon la classe apparaissant le plus fréquemment parmi ses nœuds voisins.
La figure 4 illustre le concept de graphe basé sur la similarité des images.
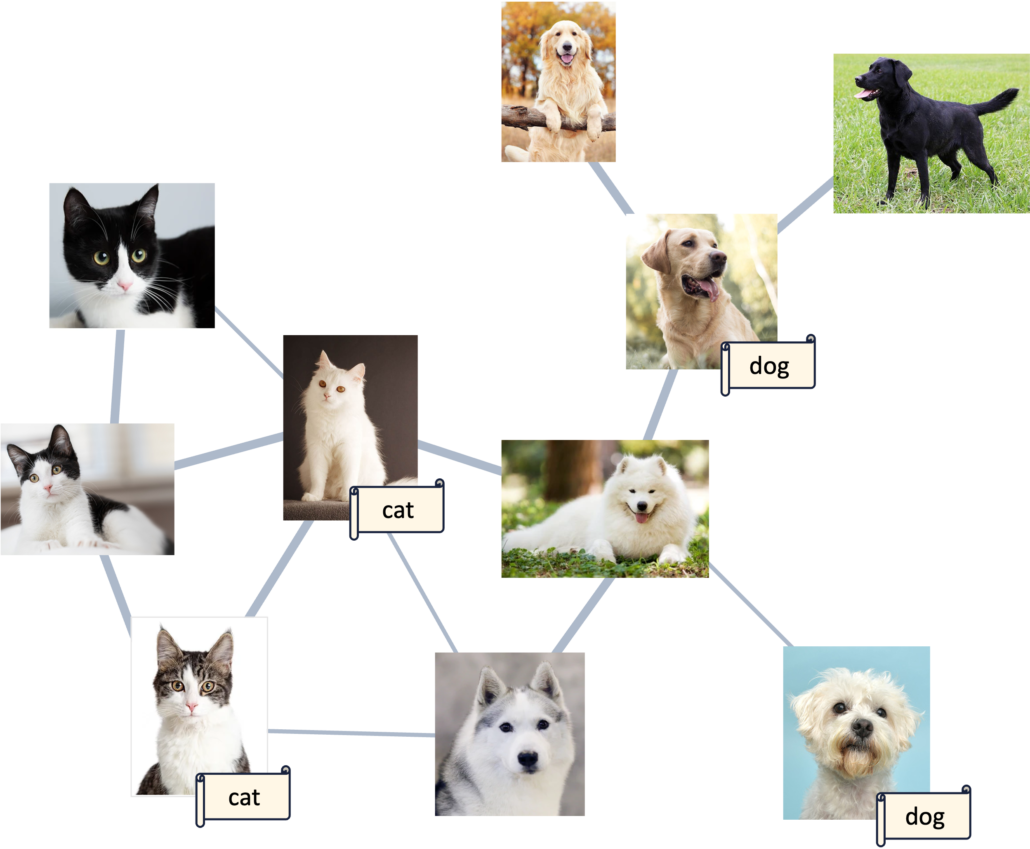
[FIGURE 4 ] – Graphe reliant les images en fonction de leur similarité.
II. ACTIVE LEARNING
Le domaine de l’active learning s’intéresse à une problématique légèrement différente de celle du SSL, bien que toujours basée sur l’exploitation des données non labellisées.
Admettons par exemple qu’après un premier entraînement du modèle (en apprentissage supervisé ou semi-supervisé), nous puissions demander à un oracle de labelliser un groupe de données parmi les données non labellisées à disposition. Le but : améliorer le modèle initial en incorporant à ses données d’apprentissage les labellisations nouvellement obtenues, et répéter ce cycle apprentissage-labellisation autant de fois que souhaité. Tout l’enjeu de ce processus repose donc sur la sélection, à chaque cycle, des données à labelliser.
L’approche la plus simple serait de choisir ces données de façon purement aléatoire. Mais, nous l’avons vu, les données non labellisées contiennent souvent des informations qu’il est pertinent de savoir extraire et exploiter. C’est cette direction que les recherches en AL se proposent d’explorer. De façon générale, la majorité des méthodes existantes se divisent en trois grands groupes, présentés ci-dessous.
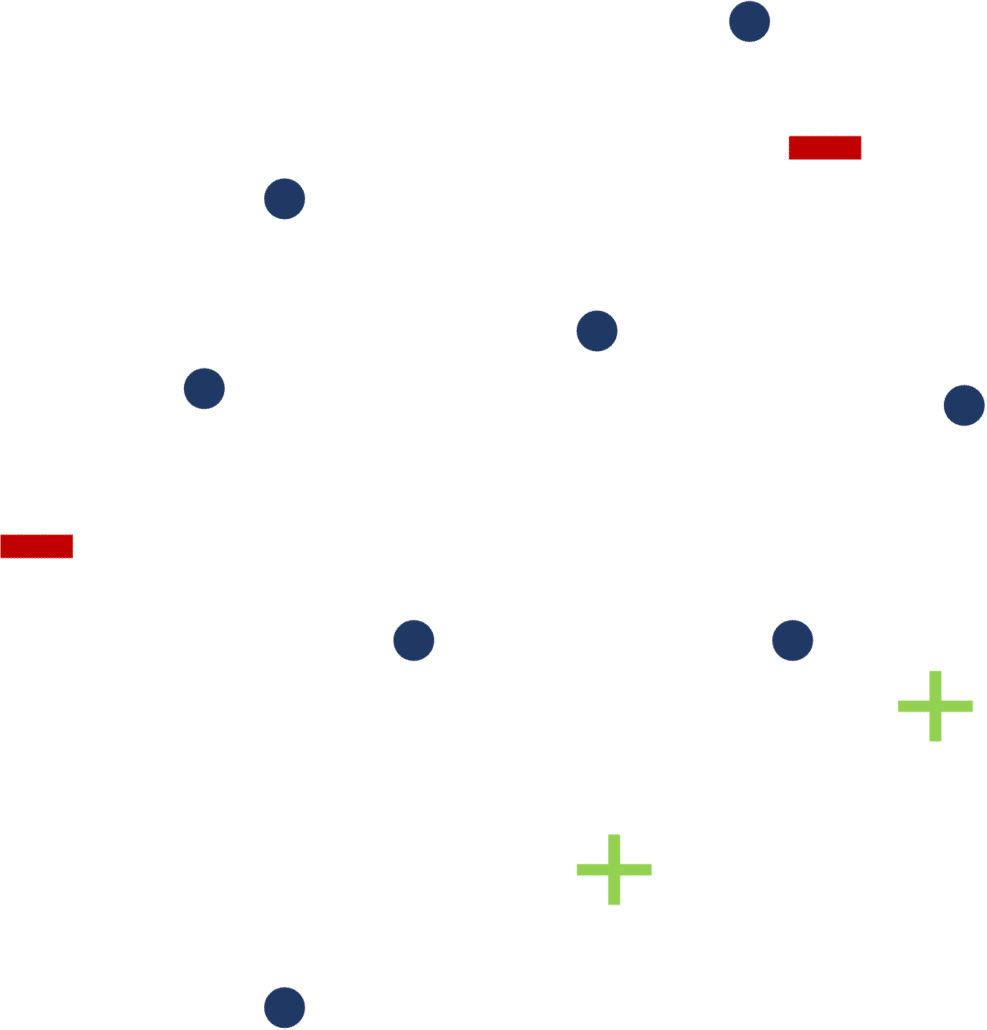
[FIGURE 5] – Comment choisir les prochains points à labelliser pour permettre l’amélioration la plus significative du modèle de classification ?
A. Incertitude
Une première approche, sans doute parmi les plus répandues, se base sur la mesure d’incertitude du modèle. En d’autres termes, on souhaite labelliser les échantillons pour lesquels le modèle est le moins sûr de lui dans ses prédictions. [6]
Pour quantifier l’incertitude d’un classifieur, on peut s’appuyer sur les probabilités qu’il affecte à chaque échantillon non labellisé d’appartenir à telle ou telle classe. Une première technique, par exemple, fait usage, pour un échantillon donné, de sa probabilité maximale (c’est-à-dire la probabilité correspondant à la classe prédite par le classifieur). Si cette probabilité est élevée, cela signifie que le classifieur a été particulièrement sûr de lui. Une faible probabilité maximale, au contraire, est le signe que la prédiction est “incertaine”, et peut donc être utilisée comme un critère de sélection des prochains échantillons à labelliser.
Dans la même veine, on peut également citer la technique de marge minimale. Ici, le critère de sélection se base non plus seulement sur la probabilité maximale, mais également sur la deuxième probabilité maximale. En d’autres termes, le critère de sélection se définit par la différence entre les deux probabilités les plus élevées parmi celles prédites par le modèle pour un échantillon donné. Si cette marge est petite, cela indique que le modèle “hésite” entre deux classes, c’est donc une mesure intéressante d’incertitude. Pour étendre ce même type de critère aux probabilités de l’ensemble des classes, on pourra par exemple opter pour une technique basée sur l’entropie (grandeur qui pourrait se résumer à une mesure de désordre ou de surprise lors d’une expérience aléatoire).
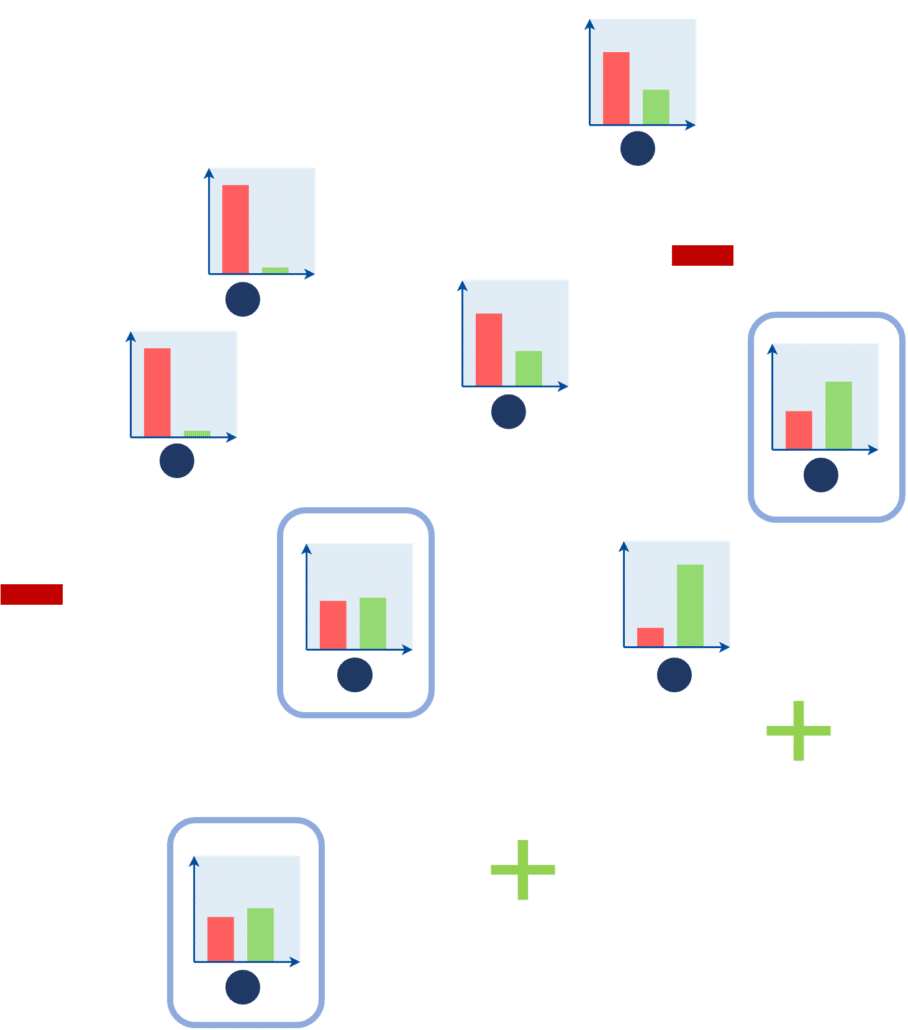
[FIGURE 6] – Echantillons à labelliser choisis par une approche basée sur l’incertitude (marge minimale).
B. Diversité
Une autre stratégie consiste à sélectionner des échantillons aussi divers que possible pour couvrir au mieux tout l’espace des inputs.
Parmi les méthodes existantes, on peut nommer celle des k-center [7], que l’on retrouve dans la théorie des graphes. De façon générale, le problème des k-center s’illustre comme suit : étant donné n villes séparées l’une de l’autre par des distances connues, où construire k magasins dans certaines de ces villes de sorte à minimiser la distance maximale entre une ville et un magasin ?
Dans notre exemple (en figure 7), employer la technique des k-center reviendrait à :
- Calculer la distance entre chaque échantillon non labellisé et l’échantillon labellisé qui lui est le plus proche.
- Sélectionner les échantillons à labelliser présentant les distances les plus grandes.
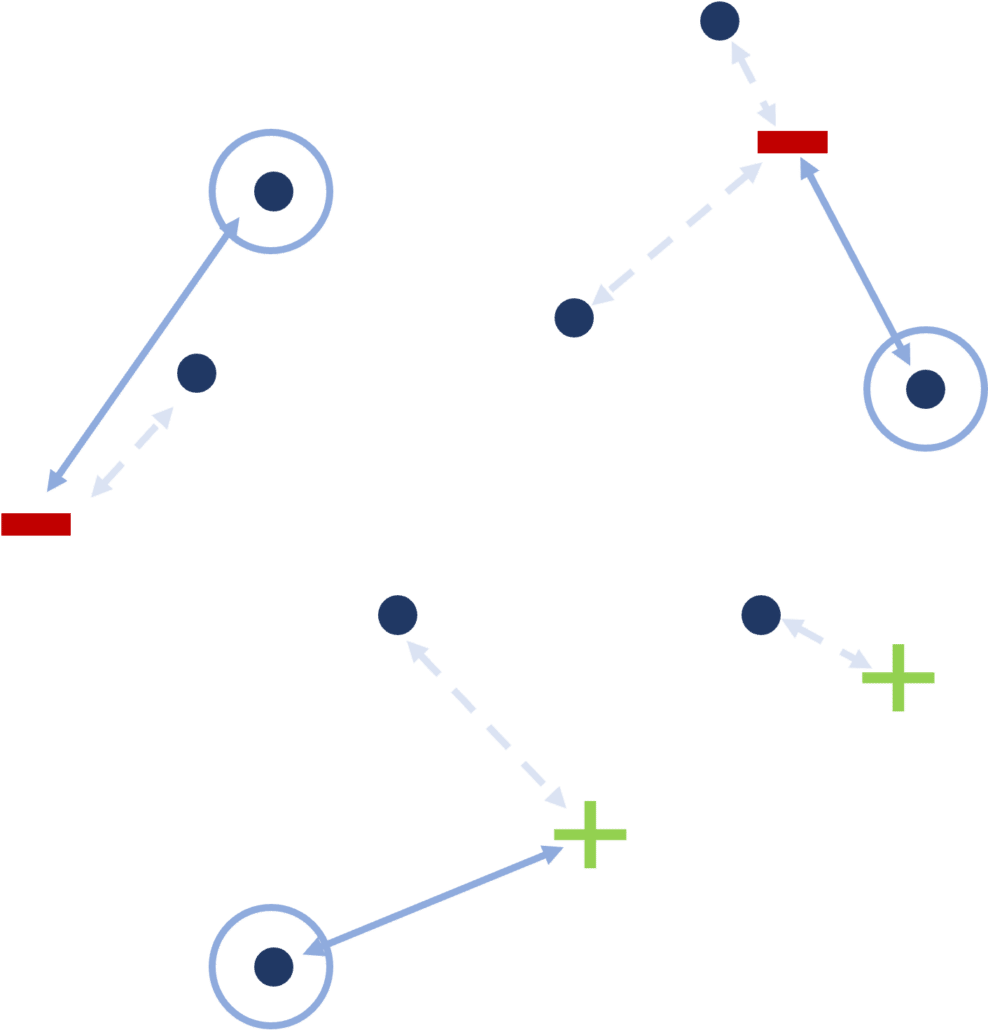
[FIGURE 7] – Echantillons à labelliser choisis par une approche basée sur la diversité (k-center).
On peut aussi penser aux approches de sélection basées sur la diversité comme une stratégie encourageant la sélection d’échantillons ne ressemblant pas aux échantillons déjà labellisés. La similarité de deux échantillons peut par exemple être évaluée via la fonction cosine similarity (ou similarité cosinus), qui calcule l’angle entre deux vecteurs à d dimensions.
C. Changement attendu
Une troisième catégorie d’approches d’AL suggère de sélectionner les échantillons qui permettront l’amélioration du modèle la plus significative, au cours de son futur entraînement. Pour ce faire, on peut par exemple mesurer l’amplitude du gradient de la loss (ou fonction coût) en fonction des paramètres du modèle.
Pour mieux illustrer ce propos, observons la figure 8. Admettons que nous entraînions un premier classifieur de façon supervisée, à l’aide des points labellisés verts et rouges. La loss à minimiser au cours de cet apprentissage, représentée en bleu sur la figure (droite), est intrinsèquement liée aux échantillons labellisés. A la fin de l’entraînement, le vecteur des paramètres définissant le modèle a une valeur que nous dénoterons ωt. Si l’on représente la loss dans l’espace des paramètres, et que nous nous plaçons au point d’abscisse ωt, nous pouvons mesurer le gradient de la loss en ce point (représenté par la flèche bleue). La question qui nous intéresse alors est : comment puis-je choisir les points qui, une fois labellisés, modifieront la loss de sorte que l’amplitude du gradient sera maximale en ce point ?
Focalisons-nous sur un échantillon non labellisé en particulier, et faisons l’hypothèse que, si je demande à un oracle de me dévoiler le label de cet échantillon, il me répondra qu’il appartient à la classe des “-” (rouge). Dans ce cas, la loss sera un peu modifiée (rouge), et son gradient au point ωt aura une amplitude différente (plus petite en l’occurrence). Si en revanche, l’oracle m’indique que l’échantillon appartient à la classe des “+” (vert), la loss évoluera différemment, et son gradient en ωt présentera cette fois une amplitude plus importante.
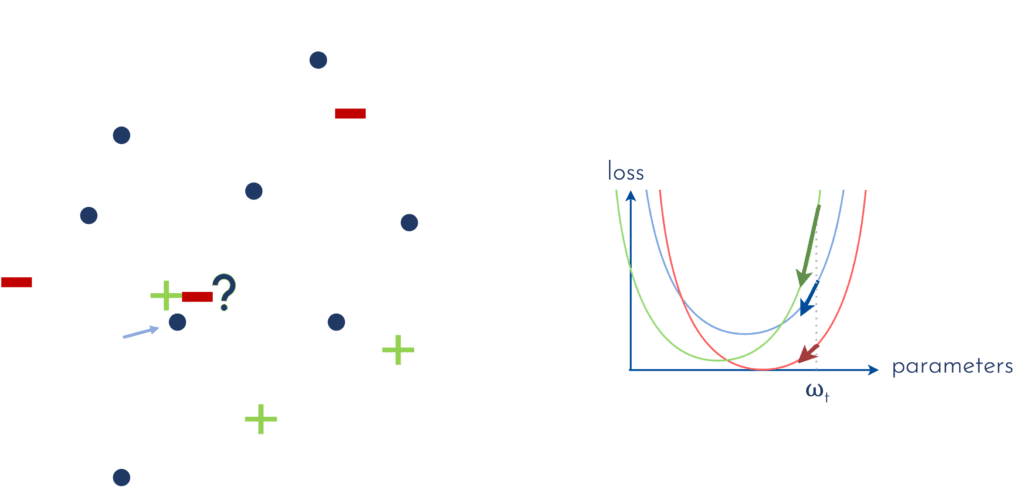
[FIGURE 8] – Mesure du gradient de la loss en fonction des paramètres du modèle, pour les différentes labellisations possibles d’un échantillon choisi.
En pratique, nous n’avons aucune idée de la réponse que nous donnera l’oracle (et c’est d’ailleurs tout l’enjeu !). Nous définissons donc le critère de sélection comme la somme des amplitudes des gradients potentiels que chaque réponse de l’oracle engendrerait, pondérée par la probabilité que l’échantillon appartienne à chacune des classes. Dans notre exemple, cela reviendrait à calculer, pour chaque échantillon E:
probabilité que E soit un “-” x longueur de la flèche rouge
+ probabilité que E soit un “+” x longueur de la flèche verte
C’est ce que l’on appelle expected gradient length [8]. Une fois ce calcul opéré pour tous les échantillons non labellisés, on sélectionne les échantillons présentant les scores les plus élevés.
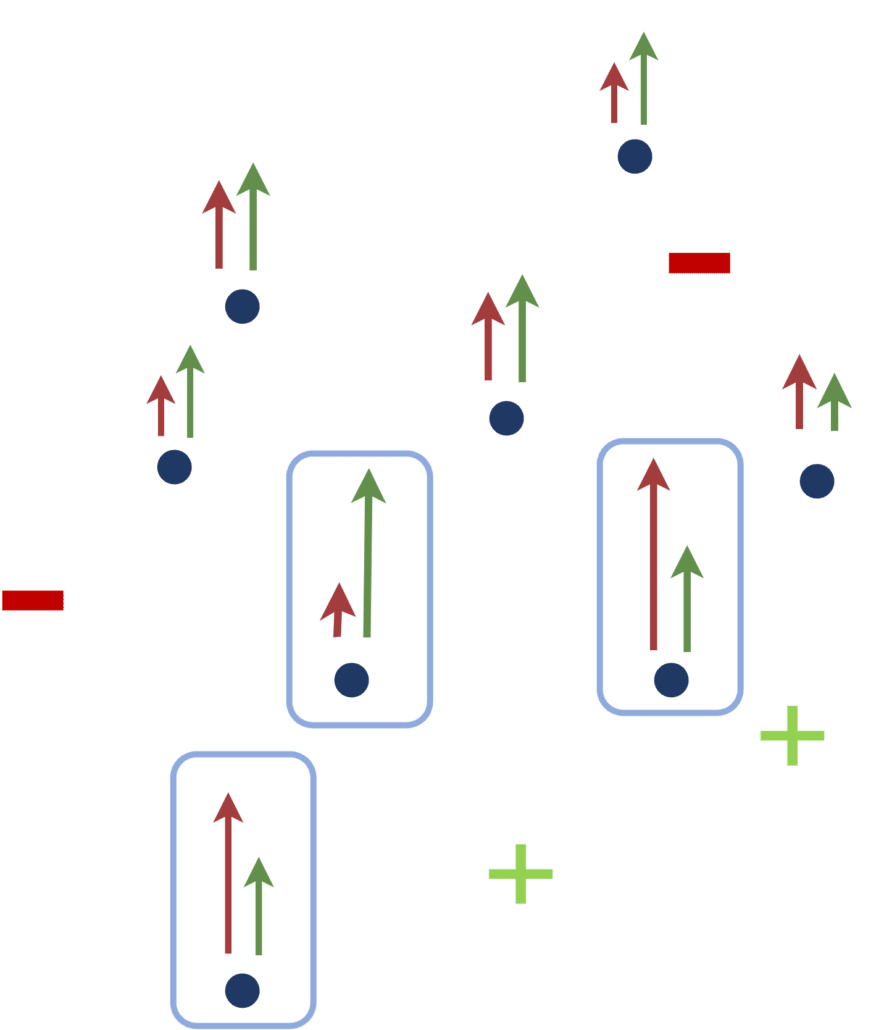
[FIGURE 9] – Echantillons à labelliser choisis par une approche basée sur l’expected gradient length.
CONCLUSION
Les approches de semi-supervised learning et d’active learning offrent des pistes intéressantes à explorer lorsque les données auxquelles on a accès ne sont que partiellement labellisées. Ces deux types de stratégies permettent en effet de tirer profit de l’information contenue dans les données non labellisées afin d’améliorer les performances du modèle final. Les premières proposent d’incorporer cette information au sein même de l’entraînement ou de la structure du modèle, tout en continuant d’exploiter les données labellisées comme c’est le cas dans un apprentissage supervisé standard. Les secondes, elles, supposent qu’un oracle pourra labelliser une portion des échantillons de façon cyclique, et guident la sélection des échantillons à labelliser, préférant ceux qui favoriseront une amélioration significative du modèle. Certains articles (relativement peu pour l’instant semble-t-il) proposent d’allier ces deux techniques pour fournir des résultats encore meilleurs. C’est le cas par exemple de [4] (classification d’images).
La problématique d’un accès à de très nombreuses données non labellisées contre peu de données labellisées se posant fréquemment en pratique (que ce soit dans les domaines industriel ou médical pour ne citer que ceux-là), il y a fort à parier que le SSL et l’AL tiendront une place importante dans l’IA de demain.







